Giao thoa sóng - Tổng hợp lý thuyết và công thức tính đầy đủ

Giao thoa sóng là gì?

Bạn đã biết giao thoa sóng là gì chưa? Điều kiện nào để quá trình giao thoa sóng có thể xảy ra? Tham khảo ngay thông tin được chúng tôi cung cấp ngay phía bên dưới đây để hiểu rõ hơn về chúng nhé.

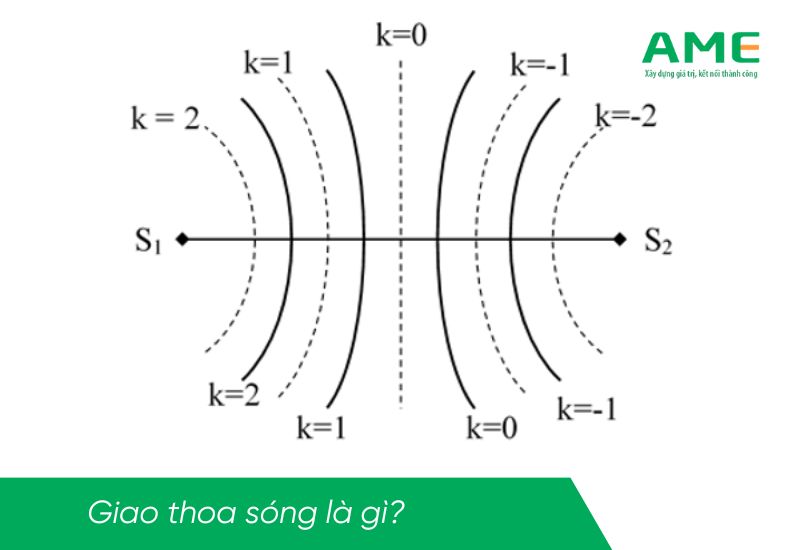
Định nghĩa giao thoa sóng

Giao thoa sóng là sự tổng hợp của hai sóng kết hợp ở trong cùng một không gian. Trong đó sẽ có những vị trí biên độ sóng bị giảm bớt hay được tăng cường thêm. Quá trình này được gọi là giao thoa sóng.

Điều kiện xảy ra giao thoa sóng

Điều kiện để có thể xảy ra trường hợp này đó chính là:

• Hai nguồn sóng phải có cùng phương hường với nhau
• Chung một tần số nhất định
• Có độ lệch pha không đổi theo thời gian

Lưu ý: Độ lệch pha không đổi theo thời gian ở đây chính là pha không chứa biến số t.

Ví dụ về hiện tượng giao thoa sóng

Quan sát hiện tượng giao thoa sóng trên mặt nước, ta quan sát thấy:

Trong vùng gặp nhau (vùng giao thoa của hai sóng) xuất hiện những điểm mà tại đó nước dao động mạnh và những điểm mà tại đó nước yên lặng (đứng yên không dao động).

Hiện đó gọi là hiện tượng giao thoa sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.

Ví dụ: Tiến hành gắn hai hòn bi nhỏ vào một thanh đàn hồi và cho chúng xuống mặt nước.

Lúc này thanh sắt sẽ bắt đầu dao động thì 2 hòn bi được gắn trên thanh sẽ tạo ra trên mặt nước 2 hệ sóng lan truyền theo được tròn đồng tâm mở rộng và trộn dần vào nhau.

Khi sóng 2 đã bắt đầu ổn định trên mặt nước thì sẽ có 2 nhóm đường cong sẽ xuất hiện. Nhóm 1 sẽ có biên độ giao động cực đại và xen kẽ với một nhóm khác tại điểm đó, mặt trước sẽ không dao động. Khi đó hiện tượng này sẽ được gọi là giao thoa của sóng.

Công thức giao thoa sóng

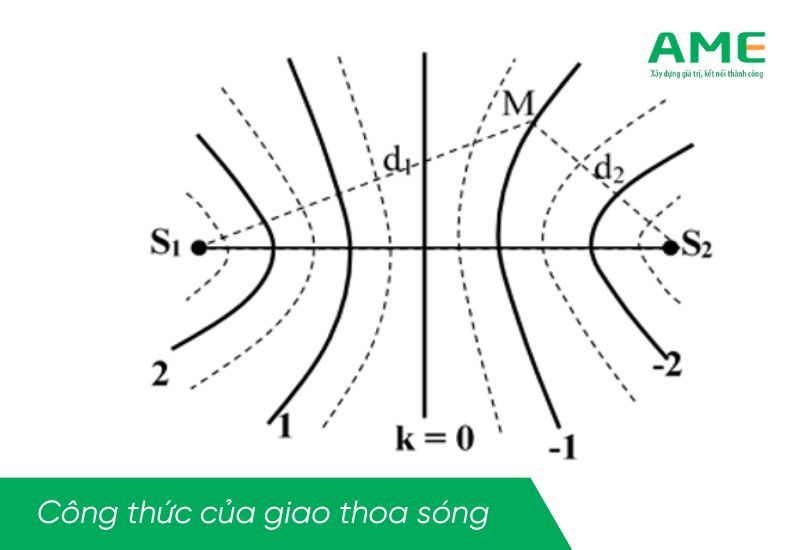
Ta xét giao thoa của 2 sóng phát ra từ hai nguồn kết hợp S1 và S2 cách nhau một khoảng cách l bất kỳ.

Phương trình sóng 2 nguồn S1 và S2:

u1 = Acos(2πft+φ1)

u2 = Acos(2πft+φ2)

Phương trình sóng tại M cách 2 nguồn S1 và S2 khoảng cách d1 và d2:

u1M = Acos(2πft+φ1 −2π d1/λ )

u2M = Acos(2πft+φ2​ −2π d2/λ)

uM = u1M + u2M = 2Acos[π(d2-d1)/λ − Δφ/2]cos[2πft−π (d1+d2)/λ + (φ1+φ2)/2]

​Biên độ dao động tại M

AM = 2A ∣cos(π(d2-d1)/λ + Δφ/2)∣ với  Δφ= φ2-φ1

Những điểm dao động với biên độ cực đại

de − d1 = kλ+(Δφ/2π)λ với k=0;±1;±2;±3;...

Những điểm dao động với biên độ cực tiểu:

d2 − d1 = (k+ 1/2 )λ+ (Δφ/2π)λ với k=0;±1;±2;±3;…

Lưu ý:

• Khoảng cách giữa 2 cực đại hoặc 2 cực tiểu liên tiếp là: λ​/2
• Khoảng cách gần nhất giữa 1 cực đại và 1 cực tiểu là: λ/4

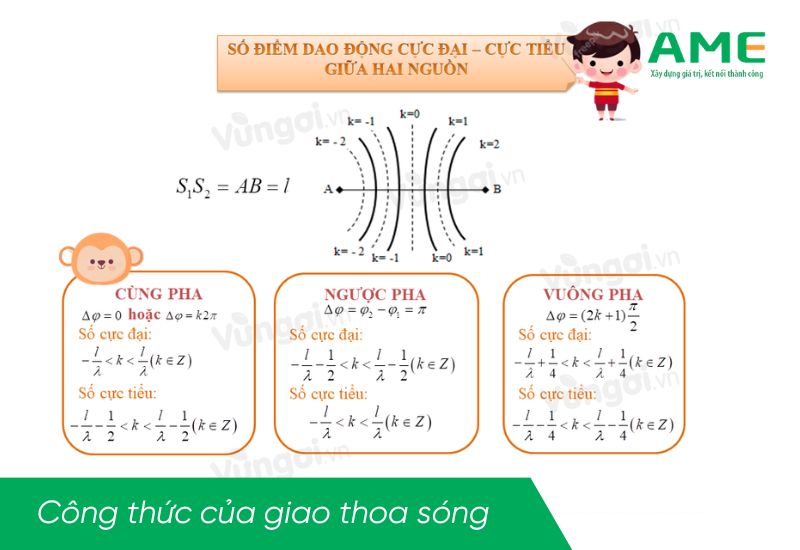
Hai nguồn dao động cùng pha

Khi hai nguồn sóng dao động cùng pha thì ∆φ = φ2 – φ1 = 0 hoặc ∆φ= 2kπ.

Phương trình giao thoa sóng tại M:

uM = u1M + u2M = 2Acos[π (d2−d1)/λ] cos [2πft−π (d1+d2)/λ+φ]

Biên độ sóng tổng hợp:A

• AMmax=2A khi: Hai sóng thành phần tại M dao động cùng pha với ∆φ=2kπ (k∈Z)

⇒∆d = d2 – d1= kλ

• A min = 0 khi: Hai sóng thành phần tại M dao động ngược pha với ∆φ=(2k+1)π (k∈Z).

⇒∆d=d2 –d1 =(k+1/2)λ

Số điểm dao động cực đại ở trên đoạn S1S2:

d1 – d2 = kλ (k ∈ Z)​

Số điểm cực đại là:

-S1S2/λ ≤ k ≤ S1S2/λ với k = 0;±1;±2;±3;…

Số điểm dao động cực tiểu trên đoạn S1S2:

d1 – d2 =( 2k +1)λ/2 (k ∈ Z)​

Số điểm cực tiểu:

-S1S2/λ – 1/2 ≤ k ≤ S1S2/λ – 1/2  với k = 0;±1;±2;±3;…

Như vậy khi hai nguồn dao động cùng pha, cùng biên độ A thì trung điểm I của đoạn S1S2 có biên độ cực đại (A max = 2A) và tập hợp của các điểm cực tiểu, cực đại là các đường Hypebol có S1, S2 là tiêu điểm.

Hai nguồn dao động ngược pha

• Phương trình giao thoa sóng tại M:

uM =u1M + u2M = 2Acos[π(d2-d1)/λ − π] cos[2πft−π (d1+d2)/λ + (φ1+φ2)/2]

• Biên độ sóng tổng hợp:

AM = 2A ∣cos(π (d2−d1)/λ −π)∣

• Điểm dao động cực đại:

d2 − d1 = (k+ 1/2 )λ​ (k ∈ Z)​

Số điểm hoặc số đường dao động cực đại trên đoạn S1S2 (không tính 2 nguồn)

-S1S2/λ – 1/2 ≤ k ≤ S1S2/λ – 1/2  với k = 0;±1;±2;±3;…

• Điểm dao động cực tiểu (không giao động):

d2 – d1 = kl (k ∈ Z)​

Số điểm hoặc số đường dao động cực tiểu trên đoạn S1S2 (không tính hai nguồn):

-S1S2/λ ≤ k ≤ S1S2/λ với k = 0;±1;±2;±3;…

Như vậy khi 2 nguồn dao động ở cùng biên độ A và ngược pha thì trung điểm của S1S2 có biên độ (cực tiểu): Amin = 0.

Hai nguồn dao động vuông pha

• Phương trình giao thoa sóng tại M:

uM =u1M + u2M = 2Acos[π(d2-d1)/λ − π/4] cos[2πft−π (d1+d2)/λ + (φ1+φ2)/2]

• Biên độ sóng tổng hợp:

AM = 2A ∣cos(π (d2−d1)/λ −π/4)∣

• Điểm dao động cực đại:

d2 − d1 = (k+ 1/4 )λ​ (k ∈ Z)​

• Số điểm hoặc số đường dao động cực đại trên đoạn S1S2 (không tính 2 nguồn)

-S1S2/λ – 1/4 ≤ k ≤ S1S2/λ – 1/4  với k = 0;±1;±2;±3;…

• Điểm dao động cực tiểu (không giao động):

d2 – d1 = (k + 3/4)λ (k ∈ Z)​

Số điểm hoặc số đường dao động cực tiểu trên đoạn S1S2

-S1S2/λ – 3/4 ≤ k ≤ S1S2/λ -3/4 với k = 0;±1;±2;±3;…

Như vậy khi cả 2 nguồn dao động ở cùng biên độ A, và vuông pha thì trung điểm của S1S2 có biên độ là: AM = A√2.

Trường hợp tổng quát

Trường hợp này sẽ xảy ra khi mà 2 nguồn có cùng tần số với nhau, khác biên độ và khác pha ban đầu.

• Phương trình tại 2 nguồn gồm:

u1 = A1cos(2πft+φ1)

u2 = A2cos(2πft+φ2​)

• Phương trình sóng tại M do 2 sóng từ 2 nguồn truyền tới

u1M = Acos(2πft+φ1 −2π d1/λ )

u2M = Acos(2πft+φ2​ −2π d2/λ)

Phương trình giao thoa sóng tại M

Sử dụng phương pháp tổng hợp hai dao động điều hòa bằng vectơ quay, ta xác định được như sau:

uM = u1M + u2M = AMcos(2πft + φM)

Trong đó: AM=

là độ lệch pha của hai dao động sóng tới tại M:  = = 2π(d2 – d1)/λ

→ | A1 – A2 | ≤ AM ≤ A1 + A2

• Điểm M dao động với biên độ cực đại AM = A1 + A2 khi và chỉ khi dao động sóng từ 2 nguồn tới M đồng pha với nhau: Δφ = 2kπ

⇔ d2 – d1 = [k +  (φ2 – φ1)/2π + 1/2] λ

• Điểm m giao động với biên độ cực tiểu AM = |A1 – A2| khi và chỉ khi dao động sóng từ 2 nguồn tới M đồng pha với nhau:  Δφ = (2k +1)π

⇔ d2 – d1 = [k +  (φ2 – φ1)/2π + 1/2] λ

• Tổng quát: Điểm M dao động với biên độ bất kỳ AM khi và chỉ khi dao động sóng từ 2 nguồn tới M lệch pha với nhau: Δφ =  + 2kπ với  thỏa mãn:

⇔ d2 – d1 = [k +  (φ2 – φ1)/2π /2π] λ

Chú ý:

Có một số điều mà bạn cần lưu ý về trường hợp giao thoa sóng tổng quát. Bạn hãy lưu ý để có thêm kiến thức hữu ích nhé.

• Trong hiện tượng giao thoa sóng thì khoảng cách ngắn nhất giữa 2 điểm dao động với biên độ cực đại (hay 2 điểm dao động với biên độ cực tiểu) trên đoạn nối hai nguồn S1S2 bằng λ/2 và giữa vực đại và cực tiểu sẽ là λ/4.
• Hai điểm cực đại gần nhau nhất sẽ dao động ngược pha với nhau.

Nguồn kết hợp và sóng kết hợp

Để hiểu rõ hơn về nguồn kết hợp và sóng kết hợp là như thế nào thì bạn có thể tham khảo và theo dõi các thông tin được chúng tôi cung cấp phí bên dưới đây. Cụ thể là như sau:

• Nguồn kết hợp: Hai nguồn được gọi là nguồn kết hợp khi chúng có cùng phương, cùng tần số, cùng pha hoặc độ lệch pha không đổi theo thời gian.

==> Người ta thường kí hiệu 2 nguồn kết hợp là A và B hoặc S1 và S2. Trong bài này, có khi Ad. dùng AB, đôi khi lại dùng S1S2 .

• Sóng kết hợp: Hai sóng kết hợp là hai sóng xuất phát ra từ nguồn kết hợp.

Như vậy là vừa rồi AME Group đã cùng bạn đi tìm hiểu về giao thoa sóng là gì cũng như các thông tin liên quan đến về khái niệm này. Hy vọng những thông tin mà chúng tôi cung cấp có thể giúp bạn hiểu rõ hơn và có được nhiều thông tin bổ ích hơn. Cảm ơn bạn đã quan tâm và theo dõi bài viết này. Hẹn gặp lại bạn trong các bài chia sẻ hữu ích tiếp theo của chúng tôi.